CREATED BY: Matt Garrod
DESCRIPTION:
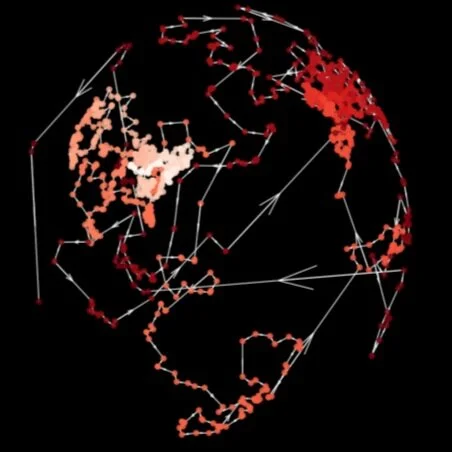
Out of the data about 11573 members I was able to find 2120 unique geographic locations. My visualisation shows a path which passes through all of the locations. At each step the walker jumps to the closest point which has not been visited previously. In the simulation we manage to visit all of the 2120 by traveling a total of 302,079 km.
This approach is far from the optimal solution which would involve solving the traveling salesman problem (https://en.wikipedia.org/wiki/Travelling_salesman_problem) on this set of points. I also cheat by allowing the walker to “tunnel” through the earth (since distances are computed from the positions in 3D space) meaning that the distance travelled is underestimated.
The Github repository at: https://github.com/MGarrod1/DVS_1YearChallenge contains an animated gif file showing the path taken as well as a Jupyter notebook in which the user can interact with and rotate the plot created.
PROCESS:
I’ve recently defended my PhD thesis - a large fraction of which is dedicated to Random Geometric Graphs (https://en.wikipedia.org/wiki/Random_geometric_graph). I thought it would be fun to make a Random Geometric Graph from the geographic positions of Data Visualization Society members. This turned out not to be very insightful as there are a large number of locations a large distance away from the others. These isolated positions end up being disconnected from the rest of the graph.
I moved on to looking at KNN graphs (https://en.wikipedia.org/wiki/Nearest_neighbor_graph) as using this type of connection rule at least removes the possibility of having many completely isolated nodes. This got me thinking about the minimum distances between individuals. As a result, I eventually ended up considering what the shortest path to visit all of the data visualisation society members would be. This is a classic problem in mathematics/computer science known as the travelling salesman problem (https://en.wikipedia.org/wiki/Travelling_salesman_problem). The solution I’ve come up with is by no means optimal, however, it at least allows you to visit all of the nodes. The points are dense enough that you can begin to see the outlines of different countries and continents!